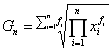avg平均数
调和平均数 <= 几何平均数 <= 算数平均数 <= 平方平均数
1、算数平均数:
又称均值,是统计学中最基本,最常用的一种平均指标,分为简单算术平均数、加权算术平均数。
应用场合:适用于数值型数据,不适用于品质数据。根据表现形式的不同,算术平均数有不同的计算形式和计算公式。
简单算术平均数适用于未分组的原始数据。加权平均数用于分组的数据。
特点 算术平均值是一个良好的集中量数,具有反应灵敏、确定严密、简明易解、计算简单、适合进一步演算和较小抽样变化的影响等特点。但是极易受极端数据的影响,每个数据的或大或小的变化都会影响最终结果。
均数(平均数)是指在一组数据中所有数据之和再除以数据的个数。例如:1,3,5,7,这四个数字的均数是〔1+3+5+7)/4〕=4。它是反映数据集中趋势的一项指标。
设一组数据为X1,X2,…,Xn,简单地算术平均数的计算公式为:

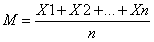
1.1、加权平均
加权算术平均:主要用于处理经分组整理数据。
设原始数据被分成K组,各组的组中值为X1,X2,…Xk,各组的频数分别为f1,f2,…fk,加权算术平均数的计算公式为:

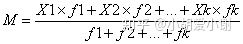
2、调和平均数:
又称倒数平均数,是总体各统计变量倒数的算数平均数的倒数。分为数学调和平均数(数值倒数的平均数的倒数)和统计调和平均数(计算结果与加权算术平均数完全相等)。
应用场合:可以用于计算平均速度.
例:计算4x100米接力赛中,运动员的总体速度。

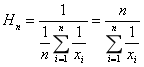
2.2 、加权调和平均数:

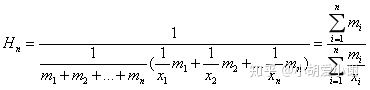

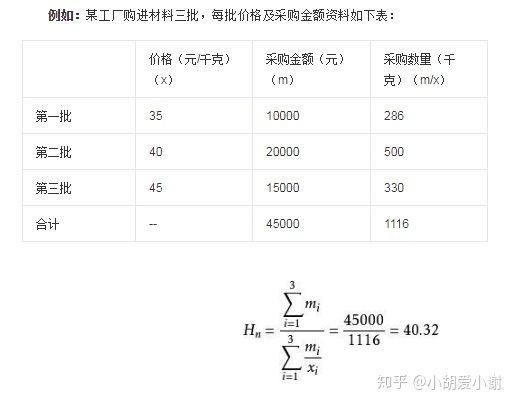
3、几何平均数:
几何平均数是对各变量值的连乘积开项数次方根。根据所拿掌握资料的形式不同,其分为简单几何平均数和加权几何平均数两种形式。
应用场合:
1、对比率、指数等进行平均;
2、计算平均发展速度;
3、复利下的平均年利率;
4、连续作业的车间产品的平均合格率;
计算总水平、总成果等所有阶段、所有环节水平、成果的连乘积总和时,求各阶段、各环节的一般水平、一般成果,要使用几何平均法计算几何平均数。
特点:
1、调和平均数易受极端值的影响,且受极小值的影响比受极大值的影响更大。
2、只要有一个标志值为0,就不能计算调和平均数。
3、当组距数列有开口组时,其组中值即使按照相邻组距计算,假定性也很大。
4、调和平均数应用的范围较小。
几何平均数是对各变量值的连乘积开项数次方根。求几何平均数的方法叫做几何平均法。如果总水平、总成果等于所有阶段、所有环节水平、成果的连乘积总和时,求各阶段、各环节的一般水平、一般成果,要使用几何平均法计算几何平均数,而不能使用算术平均法计算算术平均数。根据所拿握资料的形式不同,其分为简单几何平均数和加权几何平均数两种形式。
eg: a = 3 ,b = 4
则:几何均数c = sqr(3**2+4**2) =5
简单几何平均数:

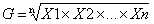
3.2 、加权几何平均数